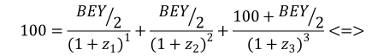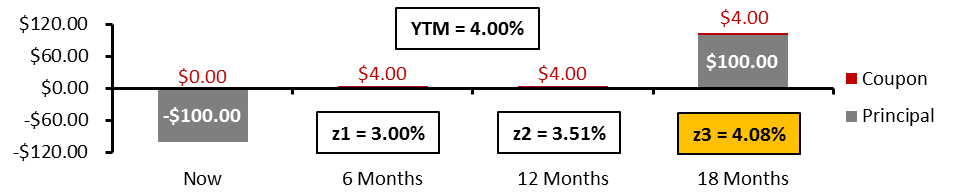Bootstrapping was one of the concepts that really annoyed me during my studies for level 1, which is silly, as it is really a rather simple concept to grasp. I just never took the time to understand it properly. I don’t want the same to happen to you, so If you spend 5 minutes now wrapping your head around it, this should bring “easy” points on the exam.
To begin with it may be a good idea to get a few principles and definitions straight:
– A coupon paying bond can be replicated by a collection of zero-coupon bonds with different principal sizes and maturities. The value of this basket of zero-coupon securities should equal the value of the coupon bearing bond, otherwise there is an arbitrage opportunity.
– The duration of a zero-coupon bond is by definition equal to its maturity (You receive all the capital as one bullet payment at the end). The duration of a coupon paying bond is by definition less than its maturity as you receive some of the capital gradually in the shape of coupon payments. If this is not clear, have a look at the bond cash flow diagrams further down in the post.
– The zero coupon rate and the spot rate refer to the same concept. I will use the term zero-coupon rate in this post.
– Finally in an attempt to trip you over, the exam writers may ask you for the bond equivalent yield (BEY) on exam day. Basically just calculate whatever the semi-annual yield is (if you are dealing with bi-annual payments) and then to get to the BEY you just multiply your semi-annual yield with 2 (needles to say you get back to your semi-annual yield by dividing with 2). If the payments are quarterly the procedure is the same but multiplying and dividing by 4. So to sum up on the exam day pay attention if the yields quoted are BEYs or not. It would be really annoying if you remember to calculate everything else correctly, but still pick the wrong answer because it needs to be quoted as a BEY and you have gone for the answer matching the semi-annual yield.
The simplest bootstrapping example that I can think of is that of the owner of two bonds issued by the same entity and both trading at par. One bond matures in 6 months and has just one payment (BEY = 6%), the other bond matures in 1 year and pays bi-annually (BEY =7%). Now based on this you may think the 1 year cash flows should be discounted at (BEY = 7%)? Not so. As we covered before the duration of your 1 year bond is less than 1 year (You receive some of your capital back already after 6 months in the shape of a coupon payment). The 7% therefore represents a weighted combination of the 6 month coupon payment discounted at the (BEY =6%) 6 month zero-coupon rate rate and the 1 year coupon and principal repayment discounted at the (BEY = ?%) 12 month zero-coupon rate. The bootstrapping technique will enable you to work out what this 12 month zero-coupon rate is, as follows:
The following charts illustrates the payment profile for the 2 coupon paying bonds described (6 and 12 months maturity respectively).
Expanding on the same methodology we can obtain the zero-coupon rate for 18 months as well.
I won’t bore you going through 20 different maturities, I think you have grasped the concept by now. Just a couple of distinctions worth noting.
You can only conduct bootstrapping if you have got a complete set of yield to maturity rates for coupon bearing bonds at par at all payment maturities up until the highest maturity length that you are looking to bootstrap. E.g. if the bonds in question pay bi-annually, you need to have a complete set of yield to maturity rates for bonds with 6, 12, 18 and 24 months to maturity in order to bootstrap the 24 month zero-coupon rate. You cannot have a gap. If there is a gap (e.g. no 24 month rate, then you won’t be able to bootstrap any zero-coupon rates longer than 18 months.
That’s it for bootstrapping. I hope my explanation made sense. If anything is still unclear please write a comment underneath or contact me directly at info@financialexamacademy.com
And finally for those bootstrapping aficionados out there (you know who you are…), I have written another post with more details and examples to bring the point home (and my own homemade formula that should hopefully make it easier for you).
Good luck with your studies!