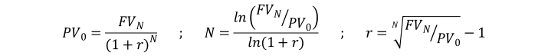The time value of money is one of the most fundamental concepts that you are going to learn at level 1. It intersects with pretty much every other quant related topic at all 3 levels, as it provides the basic translation mechanism for cash flows across different time horizons. It is therefore essential that this concept is crisp and clear in your mind.
Future value calculations can be applied to complex cash flow structures, but in essence all calculations are really based on variations of this basic formula:
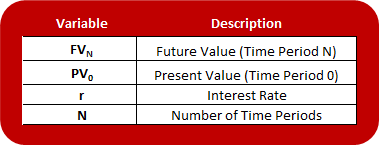
As you can see it contains 4 individual variables:
If you know the value of 3 of these variables you can easily isolate the 4th by rearranging the above formula:
In practice you won’t even have to do that, you can get your calculator to do the dirty work. I will walk through the time value of money calculator key strokes in an upcoming post.
While the ‘Number of Time Periods’ and the ‘Present/Future Value’ should be fairly self-explanatory, let’s spend a little bit of time on the ‘Interest Rate’.
Interest rates are essentially the price you pay (receive) for borrowing (lending) capital in the market place for a given period of time. Interest rates can be thought of as either a required rate of return, an opportunity cost of current consumption or a discount rate. Regardless of the perspective interest rates work as a translation mechanism in comparing cash flows carried out at different points in time.
The future is uncertain, and as you can imagine (since the interest rates bridge cash flows at different future points in time) the concept of interest rates is closely tied to risk. The nominal interest rate can be sub-divided into a real risk free rate component (you can think of this as the risk-free time value of money) as well as payment/compensation for inflation and various sources of risk to the future payment (inflation premium, default risk premium, liquidity premium and maturity premium).
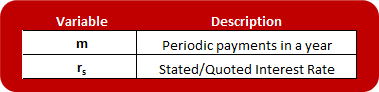
Please also note that the interest rate can be stated either as an ‘Effective Annual Rate’ (EAR) or a ‘Stated/Quoted Interest Rate’. The relationship between the two types of rates can be expressed as:
The ‘Stated/Quoted Interest Rate’ represents the annual interest rate realized based on annual compounding. Conversely the ‘Effective Annual Rate’ means exactly what it says: The actual effective annual interest rate realized (including periodic compounding). The greater the frequency of compounding the greater the difference between the two interest rate concepts. If payments are only compounded annually then the two will be equal, whereas e.g. if compounding is quarterly the EAR will be higher than the Stated/Quoted Interest Rate.
Elsewhere in the curriculum the ‘Stated/Quoted Interest Rate’ goes under different names including ‘Bond Equivalent Yield’ (BEY). This is massively confusing. Once you get the hang of the terminology however there are really just the distinction between the two concepts above that you need to learn.
As discussed it is the frequency with which the interest rate is compounded that distinguishes the ‘Effective Annual Rate’ from the ‘Stated/Quoted Interest Rate’. In theory the compounding frequency could be anywhere on the continuum between one interest payment at the end of the year/time period and continuous compounding (meaning interest is compounded an infinite number of times). I have illustrated the difference in ‘Effective Annual Rate’ depending on the compounding frequency for a 5% ‘Stated/Quoted Annual Interest Rate’ over 1 year in the chart below:
The continuous Effective Annual Rate can be calculated as:
The general time value of money formula taking account of continuous compounding is:
Now in order to avoid this becoming the longest post in the World I am going to stop here. I will follow up with a walk-through of annuities in a separate post.